Changing communicative need predicts lexical
competition and contributes to language change
Andres Karjus, Richard A. Blythe, Simon Kirby, Kenny Smith
Centre for Language Evolution, University of Edinburgh
andreskarjus.github.io | a.karjus(@)sms.ed.ac.uk
Introduction
- Hypothesis: frequency change in a word will lead to direct competition with (and possibly replacement of) near-synonym(s), unless the lexical subspace experiences high communicative need.
- Is it possible to describe some variance in terms of which successful words compete with their neighbors and which do not?
Data
522 unique words (COHA, 1890-1999) with frequency increase \(\ln\geq 2\) between any 2 successive spans of 10 years (& occur in \(\geq 2\) years & \(\geq 100\) times in the latter span).
Quantifying competition
- Embed targets into vector space (LSA) of the preceding decade, compute semantic neighbors
- Important: word occurrence probabilities sum up to 1; increase in x => decrease in y.
- The measure: where probability mass gets equalized, i.e., target increase\(\geq \sum_{}^{}\)(neighbors’ decreases). Either cosine distance, or n increasing neighbors.
- Indicates if the increasing target replaced semantically close word(s) (direct competition, obvious likely source of probability mass).
- Example: relativism, increasing +13.2pmw between 1965-1974, 1975-1984:
| word | freq. change | cumulative sum of decreases | cosine sim | normd. dist |
|---|---|---|---|---|
| relativism | +13.2 | |||
| marxism | -5.68 | 5.68 | 0.68 | 0 |
| thesis | +9.00 | 5.68 | 0.67 | 0.01 |
| jacksonian | -11.64 | 17.32>13.2 | 0.66 | 0.03 |

Communicative need
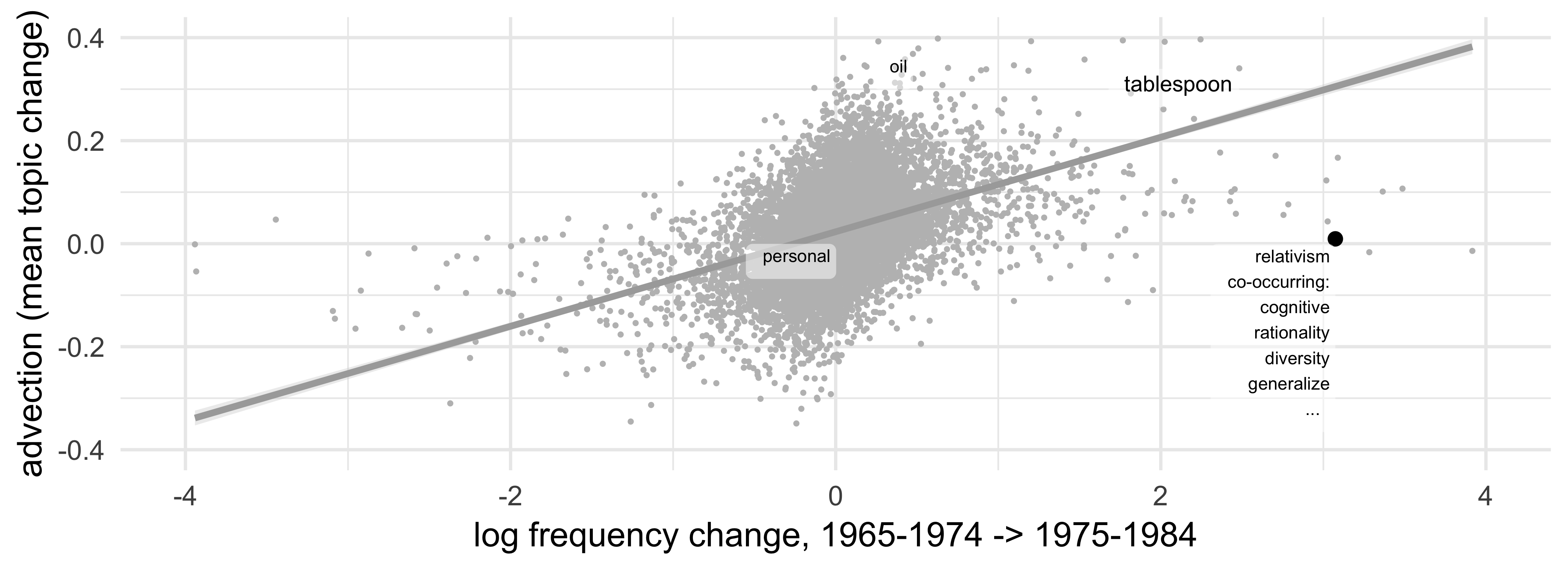
Topical advection as a proxy: weighted mean log frequency change in the top \(n\) (PPMI-weighted) context words of the target.
Results
R2=0.2. Clearer competition signal if: lower communicative need/advection (b=0.09, p<0.001), bursty series, smaller changes, a clear loser present. Also controlled for, but all p>0.05: std of yearly frequencies • semantic subspace instability • uniqueness of the form • smallest edit distance among closest sem neighbors • polsemy • leftover prob. mass • age of word in corpus • target decade.
Conclusions
Controlling for a range of factors, communicative need (operationalized by advection), describes a moderate amount of variance in competitive interactions between words: low advection words are more likely to replace a word with a similar meaning. Presumably high communicative need facilitates the co-existence of similar words.
Appendix
Notes on the competition measure
- We made sure to avoid auto-correlation between the advection measure and the dependent variable by filtering the neighbour lists of each target so that no topic word of the target (i.e. those with a PPMI>0 with the target, which are used to calculate the advection value) would be accounted for as a neighbor. This also makes sense from a semantic point of view: if two words, even if very similar occur near each other (e.g., “salt and pepper”), then it’s less palusible that they would be competing against one another. Exceptions are certainly possible, such as meta-linguistic descriptions (e.g., “vapor, previously spelled as vapour”), but we assume these would be rare.
- We also filtered out a small subset of target words with considerably higher-than-expected lexical dissemination (a proxy to polysemy, cf. Stewart & Eisenstein 2018), and those with a leftover probability mass >100% of its frequency.
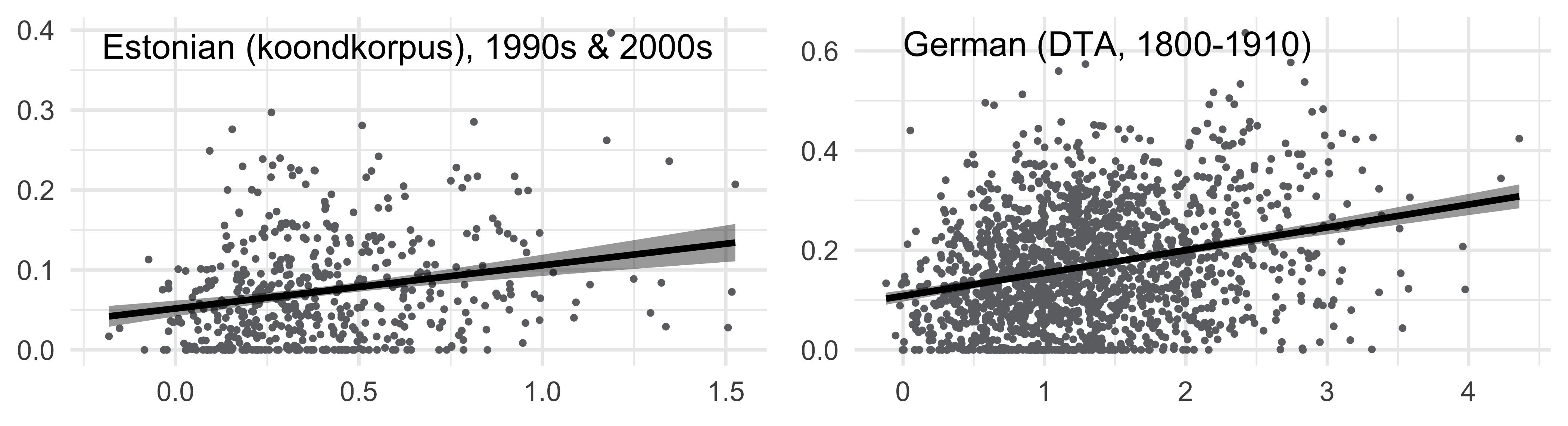
- We did not make use of the entire Corpus of Historical American English, as most of the 19th century decades are less balanced and smaller in size, the imbalance extends to the occurrence of non-standard dialects or registers in occasional year subcorpora. Similarly, we only used years after 1800 in the German corpus. The Estonian corpus only spans two decades, 1990s and 2000s, so all comparisons were done between these two, without accounting for exact starting years of each word’s increase.
- This approach certainly has limitations stemming from the imperfect nature of corpus tagging, composition balance, and vector semantics (LSA). We also disregard issues such as homonymy (although we control for polysemy in the targets) and multi-word units.
- We ran randomized baselines to make sure the observed correlation with advection is not some (unknown) artefact of the machine learning models used here. This was done by randomizing similarity matrices, i.e. each target was assigned a random list of neighbors, with random similarity values (drawn from the concatenation of all similarity vectors). After hundreds of iterations, the advection variable would come out with a p-value below 0.05 in only about 5% of the runs (i.e., as expected with an \(\alpha=0.05\)).
- Some outliers are removed on the bottom left plot on the distributions of distances and neighbors until probability mass equalized.
The polysemy measure
Details of the linear regression model for the English COHA data
| Linear regression model predicting the cosine distance (normalized by value of top neighbor) where probability mass gets equalized | |||
| Estimate | p | clearer competition signal if… | |
|---|---|---|---|
| advection | 0.0999 | <0.001 | lower comm. need |
| occurs in n years | 0.0086 | <0.001 | bursty series |
| abs. freq. change | 0.0005 | 0.011 | lower freq (change) |
| max %decrease | 0.0008 | <0.001 | a clear loser |
| R2=0.2, F=12.13(12,509), p<0.001 | |||
Also controlled for in the model, but all p>0.05: • standard deviation of yearly frequencies (burstiness) • semantic subspace instability • uniqueness of the form • smallest edit distance among closest semantic neighbors • polsemy • leftover probability mass • age of the word in the corpus • target decade.
Ongoing and future work
- We also experimented using GAMs for modelling the effect, which slightly improved descriptive power.
- Working on testing this on twitter hashtag dynamics.
- Variability in LSA vector space density is controlled for in this version by normalizing distance by the distance of the first neighbor. Another approach would be to z-score each distance using the mean and standard deviation (of the first neighbor), taken from the individual vector spaces build for each target.
References
Karjus, A., Blythe, R.A., Kirby, S., Smith, K., [to appear in Language Dynamics and Change]. Quantifying the dynamics of topical fluctuations in language.
Regier, T., Carstensen, A., Kemp, C., 2016. Languages Support Efficient Communication about the Environment: Words for Snow Revisited. PLOS ONE 11, 1–17.
Gibson, E., Futrell, R., Jara-Ettinger, J., Mahowald, K., Bergen, L., Ratnasingam, S., Gibson, M., Piantadosi, S.T., Conway, B.R., 2017. Color naming across languages reflects color use. Proceedings of the National Academy of Sciences.
Hamilton, W.L., Leskovec, J., Jurafsky, D., 2016. Diachronic Word Embeddings Reveal Statistical Laws of Semantic Change, in: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, ACL 2016, August 7-12, 2016, Berlin, Germany, Volume 1: Long Papers.
Xu, Y., Kemp, C., 2015. A Computational Evaluation of Two Laws of Semantic Change., in: CogSci.
Schlechtweg, Dominik, Stefanie Eckmann, Enrico Santus, Sabine Schulte im Walde, and Daniel Hole, 2017. German in Flux: Detecting Metaphoric Change via Word Entropy. arXiv preprint.
Petersen, A.M., Tenenbaum, J., Havlin, S., Stanley, H.E., 2012. Statistical Laws Governing Fluctuations in Word Use from Word Birth to Word Death. Scientific Reports 2.
Stewart, I., Eisenstein, J., 2018. Making “fetch” happen: The influence of social and linguistic context on nonstandard word growth and decline, in: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Brussels, Belgium, pp. 4360–4370.
Turney P.D., Mohammad S.M., 2019 The natural selection of words: Finding the features of fitness. PLOS ONE 14(1): e0211512.
The first author was supported by a Kristjan Jaak scholarship, funded and managed by Archimedes Foundation in collaboration with the Ministry of Education and Research of Estonia.